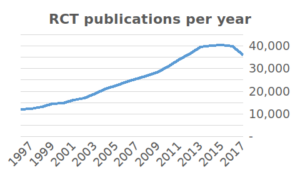
The enormous growth in clinical studies has produced a massive amount of results. As many as 285,000 clinical studies are registered on Clinicaltrials.gov since the year 2000 and over 35,000 new RCT publications were added to PubMed in 2017 alone. In recent years, there have been more and more discussions about false research findings. For example, US biotech company Amgen reported that, in an attempt to replicate 53 high-impact cancer studies, they were only able to replicate six. Some academics have therefore suggested that medical research is facing a ‘replication crisis’.
There is some truth to this statement, and some of it comes down to basic statistics. In this article, we will show that by using simple mathematics, it is possible to predict that up to 35% of published clinical research findings may be false.
What are the research findings?
As you might recall from your scruffy statistics professor, experiments are designed to test the null-hypothesis.  The null-hypothesis is the default assumption that there is no relationship among phenomena. It is rejected if your data is significantly unlikely to have occurred given the null-hypothesis. Therefore, we define a research finding as a rejection of the null-hypothesis. Note that statistical significance does not prove that a finding is true. It only tells us about the likelihood based on the data. We call this evidence.
The null-hypothesis is the default assumption that there is no relationship among phenomena. It is rejected if your data is significantly unlikely to have occurred given the null-hypothesis. Therefore, we define a research finding as a rejection of the null-hypothesis. Note that statistical significance does not prove that a finding is true. It only tells us about the likelihood based on the data. We call this evidence.
Findings can be wrong

Sometimes research findings are incorrect. Statisticians classify error in two main classes: Type I and Type II. Type I error is the mistake of reporting something as true when it is not. If we run a statistical test we typically take a confidence interval of 95% (p-value < 0.05%). While 95% confidence sounds secure, this actually means that 5%—or one in twenty—will be a false positive.
 Type II error is something that seems not true when, in fact, it is. A measure of Type II error is statistical power. Generally speaking, larger studies are more powerful. Clinical medicine typically accepts a power of 0.8. This implies that out of 10 true hypotheses tested, 2 will be falsely rejected.
Type II error is something that seems not true when, in fact, it is. A measure of Type II error is statistical power. Generally speaking, larger studies are more powerful. Clinical medicine typically accepts a power of 0.8. This implies that out of 10 true hypotheses tested, 2 will be falsely rejected.
P-values can be misleading
Based on a p-value of 0.05, we would thus expect a false positive rate of 5%. However, John Ioannidis, MD, Professor of Medicine and Statistics at Stanford University, shows with simple mathematics that the likely false positive rate of published findings is actually closer to 35%. Does this come as a surprise?
Let us perform a thought experiment: assume that from a sample of 1,000 tested hypotheses, only 100 of them will actually be true. Using a statistical significance level of 5%, we can expect that from this sample, 45 (5% of 1,000-100) will be false positives. Taking a statistical power of 0.8, only 80 (80% of 100) true hypotheses are confirmed. This leads to 125 (80 + 45) hypotheses that are seen as true. In this case, 35% (45) (not the expected 5%) of these will be false-positives!
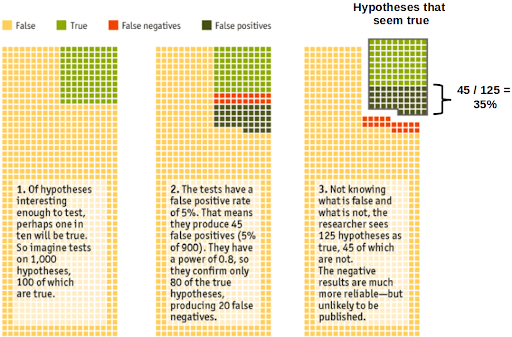
Source: Adapted from The Economist
So what does this tell us?
This demonstrates that the probability of a research finding being correct not only depends on the p-value, but also on the prior likeliness of the tested hypothesis being true. In other words, the more evidence we have that a hypothesis is true, prior to running the study, the higher the chance that a subsequent true finding is not a false positive. Let us illustrate this with an example: In the pharmaceutical industry, findings from Phase III studies are typically preceded by a Phase II study. Phase III studies will, therefore, have a lower false positive probability than the more exploratory Phase II studies.
Theory vs. practice
It is important to note that Dr. Ioannidis’ estimations are purely mathematical and not based on empirical findings. Jager and Leek rightly comment that estimates of false positive rates should be based on actual reported p-values. They found that the rate of false-positive research findings is closer to 15%. But this is still 3x higher than expected.
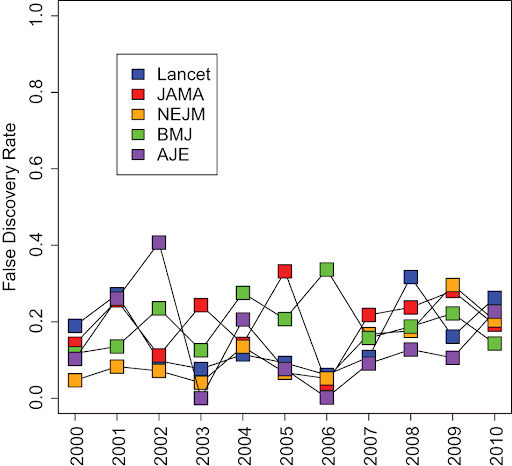
Figure: The rate of false-positive research findings is ~15%. Jager and Leek, 2014
What can be done?
Is this high false positive rate preventable? The short answer is “Yes.” However, it may require changes in our scientific mentality. Some proposed measures include:
- Raising the bar of significance from 5% to 0.5%. This reduces Type I errors but will require us to accept that fewer studies will reach statistical significance.
- Publishing studies that have not reached statistical significance will improve our understanding of success rates in different clinical fields. This allows us to better predict false-positive rates.
- Standardization of study design and data collection (e.g. using Castor EDC) will make data re-use and meta-analyses more feasible. The more relevant data points included in a study, the more powerful the study will be.
Castor EDC is a strong supporter of evidence-based medicine and is committed to open science by improving data quality and standardizing research practices. We have therefore dedicated a series of articles to better understand the issue of replicability and what we can learn from this to improve the medical research process. In the previous article, we discussed six factors that contribute to issues of replication in medical research, leading to the debate of whether or not medical research is facing a ‘replication crisis.’